Normal (geometry)

"Normal vector" redirects here. For a normalized vector, or vector of length one, see unit vector.

A polygon and two of its normal vectors.

A normal to a surface at a point is the same as a normal to the tangent plane to the surface at that point.

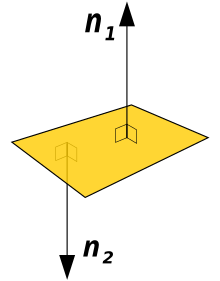
A surface normal or, simply, normal to a flat surface is a three-dimensional vector which is perpendicular to said surface. A normal to a non-flat surface at a point, p, on the surface is a vector which is perpendicular to the tangent plane to that surface at p. The word "normal" is also used as an adjective as well as a noun with this meaning: a line normal to a plane, the normal component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality.

Calculating a surface normal

For a polygon (such as a triangle), a surface normal can be calculated as the vector cross product of two (non-parallel) edges of the polygon.

For a plane given by the equation $ax+by+cz=d$, the vector $(a,b,c)$ is a normal. For a plane given by the equation r= a+αb+βc, where a is a vector to get onto the plane and b and c are non-parallel vectors lying on the plane, then the normal to the plane defined is given by bxc (the cross product of the vectors lying on the plane).

If a (possibly non-flat) surface S is parametrized by a system of curvilinear coordinates x(s, t), with s and t real variables, then a normal is given by the cross product of the partial derivatives

${\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}.$

If a surface S is given implicitly, as the set of points $(x,y,z)$ satisfying $F(x,y,z)=0$, then, a normal at a point $(x,y,z)$ on the surface is given by the gradient

$\nabla F(x,y,z).$

If a surface does not have a tangent plane at a point, it does not have a normal at that point either. For example, a cone does not have a normal at its tip nor does it have a normal along the edge of its base. However, the normal to the cone is defined almost everywhere. In general, it is possible to define a normal almost everywhere for a surface that is Lipschitz continuous.

Uniqueness of the normal

A vector field of normals to a surface.

A normal to a surface does not have a unique direction; the vector pointing in the opposite direction of a surface normal is also a surface normal. For a surface which is the topological boundary of a set in three dimensions, one can distinguish between the inward-pointing normal and outer-pointing normal, which can help define the normal in an unique way. For an oriented surface, the surface normal is usually determined by the right-hand rule. If the normal is constructed as the cross product of tangent vectors (as described in the text above), it is a pseudovector.

Uses

• Surface normals are essential in defining surface integrals of vector fields.
• Surface normals are commonly used in 3D computer graphics for lighting calculations; see Lambert's cosine law.

External link

• An explanation of normal vectors from Microsoft's MSDN