Conways Spiel des Lebens

Die Figur „Gleiter“ bildet anhand der Regeln alle vier Generationen eine verschobene Kopie ihrer selbst, wodurch sie sich „fortbewegt“.

Das Spiel des Lebens (englisch Conway’s Game of Life) ist ein vom Mathematiker John Horton Conway 1970 entworfenes Spiel, basierend auf einem zweidimensionalen zellulären Automaten. Es ist eine einfache und bis heute populäre Umsetzung der Automaten-Theorie von Stanisław Marcin Ulam.

„Spiel“ versteht sich dabei nicht als Gesellschafts- oder Kampfspiel, sondern als ein Geschehen, das nach festgelegten einfachen Regeln abläuft.

Das Spielfeld

Das Spielfeld ist in Zeilen und Spalten unterteilt und theoretisch unendlich groß. Jedes Gitterquadrat ist ein zellulärer Automat (Zelle), der einen von zwei Zuständen einnehmen kann, welche oft als lebend und tot bezeichnet werden. Zunächst wird eine Anfangsgeneration von lebenden Zellen auf dem Spielfeld platziert. Jede lebende oder tote Zelle hat auf diesem Spielfeld genau acht Nachbarzellen, die berücksichtigt werden (Moore-Nachbarschaft). Der im nächsten Schritt (Generation) vorliegende Zustand jeder Zelle ergibt sich anhand einfacher Regeln aus den Zuständen ihrer Nachbarzellen.

Das Spiel kann manuell auf einem Stück Papier oder mit Computerhilfe simuliert werden. Da ein reales Spielfeld immer einen Rand hat, muss das Verhalten dort festgelegt werden. Eine Möglichkeit besteht darin, sich den Rand durch dauertote Zellen belegt zu denken, was zu „Reflexionen“ dort anstoßender Strukturen führen kann. Eine andere Möglichkeit ist ein toroides Spielfeld, dessen Ränder an den jeweils gegenüberliegenden Rand angrenzen, so dass Zustandsänderungen, die beispielsweise hinter dem rechten Rand geschehen müssten, sich am linken Rand zeigen. Computersimulationen ermöglichen andererseits die Abbildung eines tatsächlich unendlichen Spielfeldes, indem es sich im angezeigten Rahmen unbegrenzt verschieben lässt.

Anstatt auf einer quadratisch gerasterten Ebene kann die Simulation auch auf einer sechseckig gerasterten Ebene erfolgen. Dann beträgt die Zahl der Nachbarzellen nicht acht, sondern sechs. Es gibt auch dreidimensionale Game-of-Life-Simulationen.

Eine weitere Variationsmöglichkeit ist, mehr als zwei mögliche Zustände der Gitterzellen einzuführen.

Die Spielregeln

Die Folgegeneration wird für alle Zellen gleichzeitig berechnet und ersetzt die aktuelle Generation. Der Zustand einer Zelle (lebendig oder tot) in der Folgegeneration hängt nur vom aktuellen Zustand der Zelle selbst und den aktuellen Zuständen ihrer acht Nachbarzellen ab.

Die von Conway zu Anfang verwendeten Regeln sind (lebende Zellen grün dargestellt):

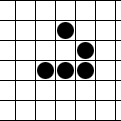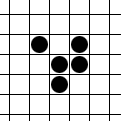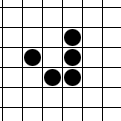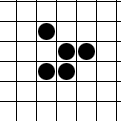
• Eine tote Zelle mit genau drei lebenden Nachbarn wird in der Folgegeneration „geboren“ (zum Leben erweckt). Hier hat die mittlere (tote) Zelle genau drei lebende Nachbarn und wird in der nächsten Generation leben:

• Eine lebende Zelle mit weniger als zwei lebenden Nachbarn stirbt in der Folgegeneration (an Einsamkeit). Hier hat die mittlere Zelle nur einen lebenden Nachbarn und wird in der nächsten Generation tot sein. Ob die Zelle rechts unten ebenfalls stirbt, hängt von ihren weiteren Nachbarn ab.

• Eine lebende Zelle mit zwei oder drei lebenden Nachbarn bleibt in der Folgegeneration am Leben. Hier hat die mittlere Zelle genau drei lebende Nachbarn und wird in der nächsten Generation weiterhin leben.

• Eine lebende Zelle mit mehr als drei lebenden Nachbarn stirbt in der Folgegeneration (an Überbevölkerung). Hier hat die mittlere Zelle fünf lebende Nachbarn und wird in der nächsten Generation tot sein. Dasselbe gilt für die mittlere Zelle der oberen Reihe, sie hat mindestens vier lebende Nachbarn. Die tote linke Zelle der mittleren Reihe hat auch mindestens vier lebende Nachbarn und wird daher in der nächsten Generation tot bleiben.

Mit diesen vier einfachen Regeln kann aus gegebenen Anfangsmustern im Laufe des Spiels eine Vielfalt komplexer Strukturen wachsen. Es gibt statische Strukturen, die sich von einer zur nächsten Generation nicht ändern, andere oszillieren, indem sie nach einer endlichen Anzahl Generationen wieder vorliegen, wieder andere wachsen oder vergehen. Manche Strukturen, sogenannte Raumschiffe, bewegen sich orthogonal oder diagonal auf dem Spielfeld fort, indem sie aufgrund der Regeln verschobene Kopien von sich selbst erzeugen.

Sogar logische Funktionen wie UND und ODER lassen sich durch bestimmte Anfangsmuster simulieren. Damit können dann sogar komplexe Funktionen der Schaltungslogik und digitalen Rechnertechnik nachgebaut werden.

Es existieren andere Varianten des Game of Life, bei denen Conways Regeln geändert oder ergänzt werden. Beispiele sind im Abschnitt Abweichende Regeln aufgeführt.

Die Objekte

Auf dem Spielfeld zeigt sich mit jedem Generationsschritt eine Vielfalt komplexer Strukturen. Einige typische Objekte lassen sich aufgrund eventuell vorhandener besonderer Eigenschaften in Klassen einteilen: sie verschwinden, bleiben unverändert, verändern sich periodisch (oszillieren), bewegen sich auf dem Spielfeld fort, wachsen unaufhörlich usw.

Statische Objekte

Statische Objekte, im Jargon auch still life („Stillleben“), sind Objekte, die sich im Spielverlauf ohne äußere Einflüsse nicht weiter verändern können, da in ihnen alle lebenden Zellen 2 oder 3 lebende Nachbarn haben und damit am Leben bleiben, während alle toten Zellen, auch in der unmittelbaren Umgebung, nicht genau drei lebende Nachbarn haben und damit tot bleiben.

Statische Objekte bleiben häufig als „Überreste“ von Wachstumsvorgängen auf dem Spielfeld zurück und bestehen unverändert fort, bis sie von einem bewegten Objekt oder einem wachsenden Bereich berührt werden.

Einige statische Objekte:

Name	Block	Beehive („Bienenstock“)	Boat („Boot“)	Loaf („Brotlaib“)	Tub („Kübel“)	Barge („Kahn“)	Pond („Teich“)	Eater(1) („Fresser“)

Der Eater(1) hat die interessante Eigenschaft, dass er einige bewegte Objekte, beispielsweise von links oben auftreffende Gleiter, durch Interaktion „fressen“ (d. h. restlos auflösen) kann und anschließend wieder an derselben Position auf dem Feld steht.

Oszillierende Objekte

Hierbei handelt es sich um Objekte, die sich nach einem bestimmten Schema periodisch verändern, d. h. nach einer endlichen Anzahl von Generationen wieder den Ausgangszustand erreichen. Befindet sich dieser neue Ausgangszustand an einer anderen Spielfeldposition, handelt es sich um ein Raumschiff (siehe unten). Oszillatoren im engeren Sinne sind stationär, behalten also ihre Position auf dem Spielfeld bei.

Die einfachste zyklische Konfiguration ist eine horizontale oder vertikale Reihe von drei lebenden Zellen. Beim horizontalen Fall wird direkt ober- und unterhalb der Zelle in der Mitte eine lebende Zelle geboren, während die äußeren beiden Zellen sterben; so erhält man eine vertikale Dreierreihe.

Eine Reihe von zehn horizontal oder vertikal aneinander hängenden Zellen entwickelt sich sogar zu einem Objekt, das einen Zyklus von fünfzehn Generationen hat, dem Pulsator.

Beispiele oszillierender Objekte sind:

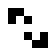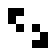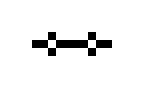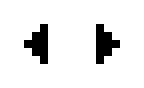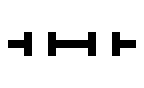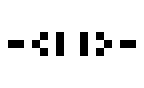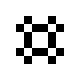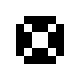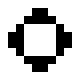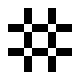
Name	Blinker	Uhr	Kröte	Bipole	Tripole	Pulsator	Tümmler	Oktagon
Zyklen	2	2	2	2	2	15	14	5

Der Pulsator wird im englischen, aufgrund eines Zyklus aus 15 Schritten, Pentadecathlon genannt. Er kann, ebenso wie oben der Eater(1), Gleiter fressen. Der Tümmler, auch Stehaufmännchen genannt, wird im englischen als Tumbler bezeichnet.

Raumschiffe und Gleiter

Raumschiffe sind (zumeist oszillierende) Objekte, die anhand der Spielregeln nach einigen Generationen in gleicher Gestalt an anderer Position des Spielfeldes erneut erscheinen und sich damit über das Spielfeld „bewegen“. Sie sind ein Beispiel der dem Spiel innewohnenden Emergenz: Die wenigen Regeln des Spiels sagen nichts über sich fortbewegende Formen aus, und doch bewirken sie genau das.

Man kann zwischen den diagonalen Raumschiffen (zum Beispiel Gleiter und Qualle) und den orthogonalen Raumschiffen (zum Beispiel Segler) unterscheiden. Diagonale Raumschiffe verschieben ihre Position in beiden Dimensionen des Spielfeldes, orthogonale nur in einer. Alle Raumschiffe bewegen sich auf einem unendlichen Spielfeld unendlich fort (solange sie auf kein anderes Objekt treffen, das ihre Replikation beeinflusst) und hinterlassen keine Spur (dann wären es Puffer).

Beispiele für Raumschiffe sind:

Gleiter
Segler(1) (LWSS) (Light-Weight Spaceship)
Segler(2) (MWSS) (Middle-Weight Spaceship)
Segler(3) (HWSS) (Heavy-Weight Spaceship)

Ablauf einer Animation dieser drei Segler

Raumschiffe haben eine strukturell bedingte Geschwindigkeit, die sich als Quotient aus der Verschiebung pro Periode und der dafür benötigten Generationenzahl ergibt. Als Bezugswert gilt die Lichtgeschwindigkeit c mit einer Zelle Verschiebung pro Periode. Beispiel: der Gleiter benötigt vier Generationen, um ein Feld weiter in der Ursprungsform zu erscheinen, und hat damit die Geschwindigkeit c/4. Die drei Segler haben auch Perioden von vier Generationen, kommen dabei aber zwei Felder weit und besitzen damit die Geschwindigkeit 2c/4 oder c/2. Da eine beliebige Struktur immer nur unmittelbar angrenzende Zellen in der folgenden Generation verändern kann, nicht aber „die übernächste“, ist eine Geschwindigkeit über c von Raumschiffen oder Wachstumsvorgängen im Spiel nicht möglich.

Das Hacker-Emblem nach Eric Steven Raymond ist vom Gleiter abgeleitet.

Gleiterkanonen

Gleiterkanonen (glider guns) sind oszillierende Objekte, die regelmäßig Gleiter erzeugen. Die erste entdeckte Gleiterkanone ist Gosper glider gun, von der alle 30 Generationen ein Gleiter wegfliegt.

Puffer

Die Puffer kann man zu den Raumschiffen zählen, wobei die Puffer im Gegensatz zu den Raumschiffen eine Spur von Objekten hinterlassen. Meist sind dies statische oder pulsierende unbewegte Objekte, es kann sich jedoch auch um Gleiter oder Segler handeln.

Andere Objekte

Daneben gibt es noch Anfangskonfigurationen, die innerhalb endlich vieler Zeitschritte ein leeres Spielfeld erzeugen.

• 
  Ein gutes Beispiel hierfür ist folgendes Startmuster
• 
  Das Muster erzeugt innerhalb von 54 Generationen eine leere Welt

Eine weitere Möglichkeit sind völlig chaotische oder explodierende Muster. Das f-Pentomino (auch r-Pentomino genannt) bewirkt trotz seiner Einfachheit ein reichhaltiges Wachstum, das über 1102 Generationen chaotisch erscheint, bis das Spielfeld vom 1103. Schritt an eine – von sechs wegfliegenden Gleitern abgesehen – oszillierende Welt bildet. Dazwischen entstehen andere interessante Strukturen, zum Beispiel ab Schritt 774 die Bienenkönigin, die zwischen zwei Hindernissen hin und her fliegen kann. Das f-Pentomimo ist das einzige rechtwinklige Objekt aus weniger als 6 lebenden Zellen, das eine so aktive Welt erzeugt, alle anderen wachsen nach spätestens 10 Generationen nicht weiter.

• 
  f-Pentomino
• 
  Verlauf

Ein anderes solches Objekt ist die Zahl 42 (mit jeder Ziffer auf 3 mal 5 Kästchen), die nach 350 Schritten einige statische und einige oszillierende Objekte sowie 2 Gleiter produziert.

Gleitersynthese

Eine Gleitersynthese (glider synthesis) ist ein gegebener Spielfeldzustand mit aus dem Unendlichen aufeinander zu fliegenden Gleitern, die in ihrer Kollision eines der anderen benannten Objekte erzeugen. Das kann über Zwischenschritte erfolgen, bei denen beispielsweise Raumschiffe ihrerseits aus Gleitern erzeugt und dann von weiteren Gleitern getroffen werden.

Für alle stationären Objekte und bis zu 14-zelligen Oszillatoren sind Gleitersynthesen bekannt.

Entwicklung aus einer zufälligen Anfangsbedingung

Die folgende Animation zeigt die ersten 1500 Entwicklungsschritte auf einem 100×100 torusförmigen Spielfeld. Die Anfangskonfiguration ist zufällig mit 31,25 % lebenden Zellen. Jeder Zustand wird 0,1 Sekunden angezeigt. Jedes Pixel steht für genau eine Zelle. Einen solchen zufälligen Anfangszustand bezeichnet man als soup (Suppe).

Sichtweisen

Die Beschäftigung mit Game of Life kann unter verschiedenen Sichtweisen erfolgen, wie etwa:

1. Das Verhalten als Gesamtes:
   Für einige Leute ist es interessant, was für ein Verhalten bestimmte Regelwelten aufweisen, zum Beispiel ob sie explodieren oder implodieren, ob sie langsam schrumpfen oder ob sie langsam „aushärten“.
2. Der biologische Aspekt: Game of Life als Mikrokosmos:
   Für andere ist Game of Life wie der Blick in ein Mikroskop. Man beobachtet die kleinen Strukturen, die man abzählen und bewerten kann. Hier freut man sich somit besonders, wenn eine neue „Lebensform“ auftaucht. Explodierende, expandierende oder gar „aushärtende“ Regelwelten sind hierbei uninteressant.
3. Der ökonomische Aspekt: Game of Life als Modell des Computerhandels der Finanzmärkte:
   Gemäß der Algorithmen des Computerhandels kauft man ein Produkt, wenn einige, aber nicht zu viele und nicht zu wenige Nachbarn es ebenfalls bereits besitzen. Wenn zu wenige es haben, verkauft man, bevor es ganz wertlos wird. Wenn zu viele es haben, verkauft man, bevor die Blase platzt.
4. Der chemische Aspekt: Energie und Materie:
   Wenn man die Häufigkeit und die Komplexität der Game-of-Life-Objekte mit dem Aufwand an Energie und Zwischenschritten vergleicht, die benötigt werden, um eine bestimmte chemische Verbindung zu erhalten, so kann man die unterschiedlichen Life-Objekte auf unterschiedliche energetische Niveaus setzen. Objekte, die bei jedem Ablauf vorkommen, wären dann auf dem Niveau von Wasser, Kohlenstoffdioxid und Natriumchlorid. Objekte, wie Unruh(2) und Fontäne, wären dann beispielsweise auf einem Niveau wie Salzsäure und Natronlauge, und Objekte wie die Segler (LWSS, MWSS und HWSS), die auch zufällig entstehen können, wären schon auf dem Niveau relativ komplexer Verbindungen.
5. Der physikalische Aspekt: Kräfte und Anfangswertproblem:
   Selbst die einfachsten physikalischen Gesetze können beliebig komplexes Verhalten als Gesamtes zeigen. Rein deterministisch/mechanisch können (beliebig) kleine Abweichungen der Startbedingung zu ganz unterschiedlichen Ergebnissen führen. Somit lässt sich ein Anfangswertproblem formulieren, worauf chaotisches Verhalten folgt. Es folgen Endzustände, Schwingungen, Wachstum, aber auch dauerhaft unregelmäßiges Verhalten.
6. Game of Life als Automat:
   Es gibt den Typus des Game-of-Life-Interessierten, der hauptsächlich an der Konstruktion von Automaten interessiert ist, also solchen Strukturen, die wie eine Maschine oder Fabrik arbeiten. Es gibt einen Verband aus Strukturen, der entfernt Ähnlichkeit mit einem Rollfeld eines Flughafens hat, auf dem ständig Flugzeuge starten, und dazwischen die Fahrzeuge, die den Betrieb aufrechterhalten, zu ihren Stationen fahren.
7. Game of Life als Rechnermodell: Es ist möglich, mithilfe komplexer Startmuster eine Universelle Turing-Maschine und deren Eingabe zu modellieren. Conway’s Game of Life ist damit Turing-vollständig. Theoretisch lässt sich jedes algorithmische Problem, das man mit einem Computer lösen kann, auch allein durch Game of Life berechnen.
8. Game of Life in der Theoretischen Informatik als Entscheidungsproblem:
   Man kann zeigen, dass es keinen Algorithmus gibt, der als Eingabe zwei beliebige Game-of-Life-Konfigurationen erhält und in allen Fällen entscheiden kann, ob eine Konfiguration aus der anderen entstehen kann oder nicht. Diese Frage ist damit unentscheidbar.

Conways Herausforderung

Conway bot demjenigen einen Preis von 50 US-Dollar, der nachweisen konnte, dass mit Conways Spiel des Lebens unbegrenztes Wachstum möglich ist. Da für einen eindeutigen Beweis ein geordnetes Wachstum notwendig ist, waren die chaotischen explosionsartigen Vermehrungen ungeeignet.

Die erste Lösung für dieses Problem – eine so genannte Gleiterkanone, die in regelmäßigen Abständen einen Gleiter hervorbringt – wurde 1970 von dem amerikanischen Mathematiker Bill Gosper präsentiert. Der Gleiter erzeugt innerhalb von vier Generationen eine verschobene Kopie von sich selbst, und somit kann die Kanone an derselben Stelle den nächsten Gleiter erzeugen.

Es ist möglich, aus Kollisionen von Gleitern eine Gleiterkanone zu erzeugen. Damit kann die Bewegungsrichtung der Gleiter geändert werden, und es besteht die theoretische Möglichkeit, selbstreplizierende Automaten zu konstruieren.

GOSPERs Gleiterkanone (obere Bildhälfte); die erzeugten Gleiter fliegen nach rechts unten und werden dort von einem Pulsator (siehe unter Oszillatoren) liquidiert.

In der oberen Bildhälfte befindet sich die Gleiter-Kanone, die in 30 Generationen einmal pulsiert und dabei einen Gleiter erzeugt. Im rechten, unteren Teil des Bildes befindet sich der Gleiter-Fresser, der in 15 Generationen einmal pulsiert und bei jeder zweiten Pulsation einen Gleiter zerstört. Die Gleiter bewegen sich von der Bildmitte nach rechts unten. Links unten läuft der Generationen-Zähler mit. In der Bildbeschreibung befinden sich Links zu dem die Animation erzeugenden GW-BASIC-Programm und zu den Startdaten.

Mittlerweile wurden unüberschaubar viele Konstellationen gefunden, die ähnlich wie die einfache Gleiterkanone laufend Zellen produzieren. Neben Gleitern und verschiedenen Seglern sind sogar komplexe Kanonen gefunden worden, die selbst Gleiterkanonen „feuern“. Zusammen mit anderen nützlichen Gebilden, wie sich fortbewegende Kanonen, Gleiter-Reflektoren oder Relays (Gebilde, die etwa Gleiter für einige Generationen bremsen), bilden sie Werkzeuge für das Entwerfen komplexer Automaten wie etwa der Turingmaschine. Dies beweist, dass Conway’s Game of Life Turing-vollständig ist.

Im Jahr 2012 wurde erstmals eine Konstellation vorgestellt, die in der Lage ist, ein Spielfeld zu simulieren, das den Regeln von Conways Spiel des Lebens entsprach (Selbstsimulation).

Abweichende Regeln

Kopierwelt

Zyklus 112

Man kann sich abweichende Regeln zum klassischen Game of Life vorstellen. Das folgende Regelwerk definiert beispielsweise ein sich reproduzierendes System, eine „Kopierwelt“.

• Todes-Regel: Eine Zelle mit genau 0, 2, 4, 6 oder 8 lebenden Nachbarn stirbt (oder bleibt tot).
• Geburts-Regel: 1, 3, 5 oder 7 lebende Nachbarn erzeugen (oder erhalten) eine lebende Zelle.

Diese Regeln kann man auch als „Anzahl Modulo 2“ zusammenfassen.

Wenn man in dieser Kopierwelt zum Beispiel eine Struktur in Form des Buchstaben H zeichnet, so werden lauter identische H-Buchstaben erzeugt. Bei größeren Ausgangsmustern sorgt dieses Regelwerk sogar selbständig für ein Auseinanderrücken der vorher kollidierenden Kopien. Die Kopien der Ausgangsmuster treten bei Zyklennummern auf, die ein Vielfaches von 4 sind. Bei größeren Ausgangsmustern treten sie aber nicht bei jedem Vielfachen von 4 auf. Wendet man diese Regel auf ein Feld der Größe 15×15 an, so sterben nach der 15. Generation immer alle Zellen aus.

Um sich beim Vergleich verschiedener Regelwerke eine umständliche Umschreibung der Regeln zu ersparen, existiert eine Kurzschreibweise für die Regeln von Game of Life: Man setzt zunächst (in aufsteigender Reihenfolge) die Ziffern der Anzahl von Nachbarn aneinander, bei der eine Zelle überlebt, und anschließend, durch einen Schrägstrich abgetrennt, die Ziffern, die den Werten entsprechen, bei der eine Zelle geboren wird. Die klassische Conway-Welt wird also durch 23/3 beschrieben, die oben beschriebene Kopierwelt durch 1357/1357. Es wurden auch Regeln für mehrdimensionale Räume entwickelt. Hier entstehen aber natürlich Darstellungsprobleme. Sehr dicht an das Verhalten nach dem klassischen 23/3-Regelwerk von Conway (zwei oder drei Nachbarn erhalten eine Zelle, drei Nachbarn erzeugen eine neue Zelle) kommen die Regelwerke 34/3 und 35/3. Die Anzahl aller möglichen Regelwerke ergibt sich aus der Anzahl der Möglichkeiten, Ziffern zwischen 0 und 8 vor und nach dem Schrägstrich auszuwählen. Insgesamt sind daher ${2^{9}}\cdot {2^{9}}=2^{18}=262144$ Regelwerke denkbar, von denen die meisten jedoch nur wenige, triviale Eigenschaften aufweisen. Einige der interessanteren Regelwerke werden im Folgenden beschrieben.

Die 3/3-Welt

Bisher ist für dieses Regelwerk nur ein statisches Objekt bekannt, welches sich nicht aus anderen statischen Objekten zusammensetzt. Dieses Objekt ist der auch im 23/3-Regelwerk statische 2×2-Block:

Quadro

Da jede Zelle dieses Blocks genau 3 Nachbarn hat, ist er trivialerweise ein statisches 3/3-Objekt. Die Zwei-Nachbarn-Regel des klassischen 23/3-Regelwerk von Conway spielt für den Block also keine Rolle.

In der 3/3-Welt gibt es zum Beispiel diese oszillierenden Objekte:

Pedal		Kegel		Unruh(1)		Strudel

Außer Unruh(1) sind diese Objekte unter allen möglichen Regelwerken bis 345678/3 statisch, insbesondere auch bei den unten besprochenen 34/3- und 35/3-Regelwerken. Unruh(1) funktioniert unter allen Regelwerken, in denen 3/3 enthalten ist und 0/0124 nicht (damit also auch in der Conway-Welt, dem 23/3-Regelwerk). Solche Objekte kann man als Wanderer bezeichnen.

Die meisten anderen Objekte können in der 3/3-Welt allerdings nicht überleben, so dass sich das Spielfeld bei zufälligen Startbedingungen meistens innerhalb von wenigen Generationen bis auf ein paar wenige Teile komplett leert.

Die 13/3-Welt

Dies ist eine Regelwelt mit wenigen oszillierenden Objekten.

Wenigstens die drei folgenden, oszillierenden Objekte sind bekannt:

Pingpong	O1G3(2) (Zweites oszillierendes Objekt in der 1G3-Welt, auch als O13-3(2) schreibbar)
Pseudo-Gleiter

Als eine Variante der 13/3-Regelwelt kann man die 135/35-Regelwelt betrachten.

Die 34/3-Welt

Oszillierende Objekte der 34/3-Welt:

Strange

Frosch

O4G3(3)

O4G3(4)

Pedal

Kegel

Unruh(1)

Strudel

Während für Strange und Frosch das 34/3-Regelwerk wichtig ist, sind Pedal, Kegel, Unruh(1) und Strudel auch in der 3/3-Welt oszillierend.

Die 35/3-Welt

In der 35/3-Welt gibt es zum Beispiel diese drei sich bewegenden Objekte:

Schwimmer(1) und Schwimmer(2)

35/3-Segler

Ebenso wie in der 34/3-Regelwelt kommen die oszillierenden Objekte Pedal, Kegel, Unruh(1) und Strudel in der 35/3-Regelwelt vor.

Die 2/3-Welt

Diese Regelwelt hätte eigentlich an die erste Stelle gehört, da sie ein wichtiges oszillierendes Objekt enthält, das eigentlich der 23/3-Welt, also Conways Life zugeordnet wird, zu der es kompatibel ist:

O2-3(1)		Unruh(2)

Damit existieren wenigstens drei oszillierende Objekte, inklusive Unruh(1), die fälschlicherweise exklusiv Conway’s Game of Life (23/3) zugeordnet werden.

Die 24/3-Welt

statische Objekte:

oszillierende Objekte:

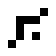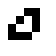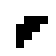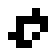
O24-3(1)		O24-3(3)		Seegurke		O24-3(4)

Die 245/3-Welt

Neben den oszillierenden Objekten, die auch in der 24/3-Regelwelt vorkommen, existieren hier auch noch ein paar andere oszillierende Objekte:

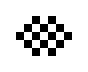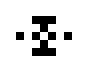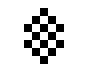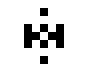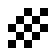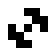
O245-3(1)	O245-3(2)

Das besondere aber ist das Vorkommen eines sich bewegenden 7-Zyklen-Objekts, das in seiner Art der Bewegung einer Qualle ähnelt:

Qualle

Die 125/36-Welt

In der 125/36-Regelwelt existieren diese beiden oszillierenden Strukturen:

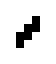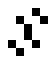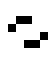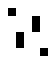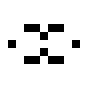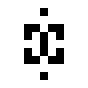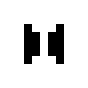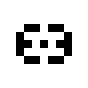
O125-36(1)	O125-36(2)

Antiwelten

Zu jeder Regelwelt gibt es eine Antiregelwelt, in der Form, dass alles invertiert ist. Also alle Zellen, die sonst tot sind, leben, und alle Zellen, die sonst leben, sind tot. Dies zeigt sich im Ablauf durch ein schwarzes Feld, auf dem die Strukturen weiß sind.

Um eine solche Antiregelwelt zu erzeugen, kann man die Regeln in Form eines Schalterfeldes darstellen:

	0	1	2	3	4	5	6	7	8
G
T

• G steht für Geburt.
• T steht für Tod.

Die folgende Belegung bedeutet, dass bei drei Nachbarn eine tote Zelle lebendig wird und eine lebende Zelle bei keinem oder einem sowie bei vier bis acht Nachbarn stirbt und ansonsten der Zustand einer Zelle unangetastet bleibt:

Conway-Regeln

	0	1	2	3	4	5	6	7	8
G
T

Wenn man die Zustände des Schalterfelds um 180° rotiert (nicht spiegelt oder kippt), erhält man die Antiregeln:

Anti-Conway-Regeln

	0	1	2	3	4	5	6	7	8
G
T

Alternative Regel-Bezeichnung

Regel-Bezeichnung		Kommentar
3/3	G3
13/3	1G3
23/3	2G3	Conways Original-Game of Life
34/3	4G3
35/3	5G3
236/3	26G3	explodierend, teilweise mit den Strukturen aus 23/3
135/35	1G35	erweitertes 13/3
12345/3	1245G3	eine Welt, in der ein sich ausbreitendes, labyrinthartiges Muster entsteht
1357/1357	G1357	ein Kopiersystem, wobei sich aus einfachen kleinen Strukturen komplexe Muster entwickeln können
24/35	—
0123/01234	—	eine blinkende Fleckenwelt

Anti-Regeln		Kommentar
01234678/0123478	6G0123478	Anti-Conway
01234678/0123678	4G0123678	Anti-4G3
02468/02468	G02468	Anti-Kopiersystem

Ineinander übergehende Regelwelten

Denkbar sind Game-of-Life-Simulationen, bei denen abgegrenzte Bereiche (zum Beispiel linke und rechte Seite) jeweils einer anderen Regelwelt unterzogen werden. Dabei könnte man sich bewegende Wanderer, die in beiden Regelwelten existieren können, aufspüren.

Siehe auch

• Conway-Folge
• Kombinatorische Spieltheorie

Weblinks

Commons: Game of Life – Album mit Bildern, Videos und Audiodateien

• Ausführliches Wiki über Conway’s Game of Life (englischsprachig)
• Das Game of life simuliert das Game of life, Video
• Game of life dreidimensional (2015), Video
• Game of Life Universal Turing Machine, Video
• Game of Life, Quelltext mit ThreeJS (JavaScript)

Simulationen

• Video: Conway's Game of Life auf einem Intel 8008 Rechner (K1510) von ROBOTRON (1kByte code, 1kByte RAM) programmiert im Jahre 1980. Aufgenommen im ROBOTRON Computer-Museum.
• Play John Conway’s Game of Life, interaktive Simulation mit frei setzbaren Anfangszuständen
• Eine Implementierung von Conway's Game of Life in JavaScript
• NetLogo enthält in der mitgelieferte „Models Library“ die Simulation Life.

Java-Applikationen

• www.denkoffen.de/Games/SpieldesLebens/ (Applet)
• www.ibiblio.org/lifepatterns (Applet)
• www.hexatron.com/hexca (hexagonal) (Applet)
• www.gridlife.info (Download)

Implementiert in Brainfuck

• linusakesson.net

Literatur

• Nathaniel Johnston und Dave Greene: Conway's Game of Life. Mathematics and Construction. 2022. ISBN 978-1-7948-1696-1. Online verfügbar (PDF; 91 MB).
• Alex Stone: Math’s ‘Game of Life’ Reveals Long-Sought Repeating Patterns. In: Quanta Magazine, 18. Januar 2024. Online verfügbar