Polygon triangulation
In computational geometry, polygon triangulation is the decomposition of a polygonal area (simple polygon) P into a set of triangles,[1] i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P.
In the strict sense, these triangles may have vertices only at the vertices of P. In a less strict sense, points can be added anywhere on or inside the polygon to serve as vertices of triangles. In addition, the cases of triangulation of a simple polygon and of a polygonal area with polygonal holes are treated separately.
Triangulations may be viewed as special cases of planar straight-line graphs. When there are no holes or added points, triangulations form maximal outerplanar graphs.
Polygon triangulation without extra vertices
Over time a number of algorithms have been proposed to triangulate a polygon.
Special cases
A convex polygon is trivial to triangulate in linear time, by adding edges from one vertex to all other vertices.
A monotone polygon can easily be triangulated in linear time with either the algorithm of A. Fournier and D.Y. Montuno,[2] or the algorithm of Godfried Toussaint[3].
Ear clipping method

One way to triangulate a simple polygon is based on the fact that any simple polygon with at least 4 vertices without holes has at least two so called 'ears', which are triangles with two sides being the edges of the polygon and the third one completely inside it (and with an extra property unimportant for triangulation).[4] The algorithm then consists of finding such an ear, removing it from the polygon (which results in a new polygon that still meets the conditions) and repeating until there is only one triangle left.
This algorithm is easy to implement, but suboptimal, and it only works on polygons without holes. An implementation that keeps separate lists of convex and concave vertices will run in O(n2) time. This method is known as ear clipping and sometimes ear trimming. An efficient algorithm for cutting off ears was discovered by Hossam ElGindy, Hazel Everett, and Godfried Toussaint.[5]
Using monotone polygons
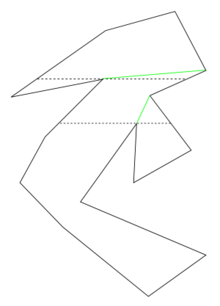
A simple polygon may be decomposed into monotone polygons as follows.[1]
For each point, check if the neighboring points are both on the same side of the 'sweep line', a horizontal or vertical line. If they are, check the next sweep line on the other side. Break the polygon on the line between the original point and one of the points on this one.
Note that if you are moving downwards, the points where both of the vertices are below the sweep line are 'split points'. They mark a split in the polygon. From there you have to consider both sides separately.
Using this algorithm to triangulate a simple polygon takes O(n log n) time.
Computational complexity
For a long time there was an open problem in computational geometry whether a simple polygon can be triangulated faster than O(n log n) time.[1] In 1990 David G. Kirkpatrick, Maria M. Klawe, Robert E. Tarjan discovered an O(n log log n) algorithm for triangulation. Simple randomised methods such as Seidel's [6] or Clarkson et al's, have O(n log* n) behaviour which, in practice, are indistinguishable from O(n).
Bernard Chazelle showed in 1991 that any simple polygon can be triangulated in linear time, though the proposed algorithm is very complex.[7]
The time complexity of triangulation of a polygon with holes has an Ω(n log n) lower bound.[1]
See also
- Catalan number
- Point set triangulation
- Delaunay triangulation
- Minimum-weight triangulation, for a point set and for a simple polygon
References
- ^ a b c d Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000), Computational Geometry (2nd revised ed.), Springer-Verlag, ISBN 3-540-65620-0
{{citation}}: CS1 maint: multiple names: authors list (link) Chapter 3: Polygon Triangulation: pp.45–61. - ^ Fournier, A.; Montuno, D. Y. (1984), "Triangulating simple polygons and equivalent problems", ACM Transactions on Graphics, 3 (2): 153–174, doi:10.1145/357337.357341, ISSN 0730-0301
- ^ Toussaint, Godfried T. (1984), "A new linear algorithm for triangulating monotone polygons," Pattern Recognition Letters, 2 (March):155-158.
- ^ Meisters, G. H., "Polygons have ears." American Mathematical Monthly 82 (1975). 648-651
- ^ ElGindy, H., Everett, H., and Toussaint, G. T., (1993) "Slicing an ear using prune-and-search," Pattern Recognition Letters, 14, (9):719-722.
- ^ Seidel, Raimund (1991), "A Simple and Fast Incremental Randomized Algorithm for Computing Trapezoidal Decompositions and for Triangulating Polygons", Computational Geometry: Theory and Applications, 1: 51–64
- ^ Chazelle, Bernard (1991), "Triangulating a Simple Polygon in Linear Time", Discrete & Computational Geometry, 6: 485–524, doi:10.1007/BF02574703, ISSN 0179-5376
- Amato, Nancy M.; Goodrich, Michael T.; Ramos, Edgar A. (2001), "A Randomized Algorithm for Triangulating a Simple Polygon in Linear Time", Discrete & Computational Geometry, 26 (2): 245–265, doi:10.1007/s00454-001-0027-x, ISSN 0179-5376
External links
- Demo as Flash swf, A Sweep Line algorithm.
